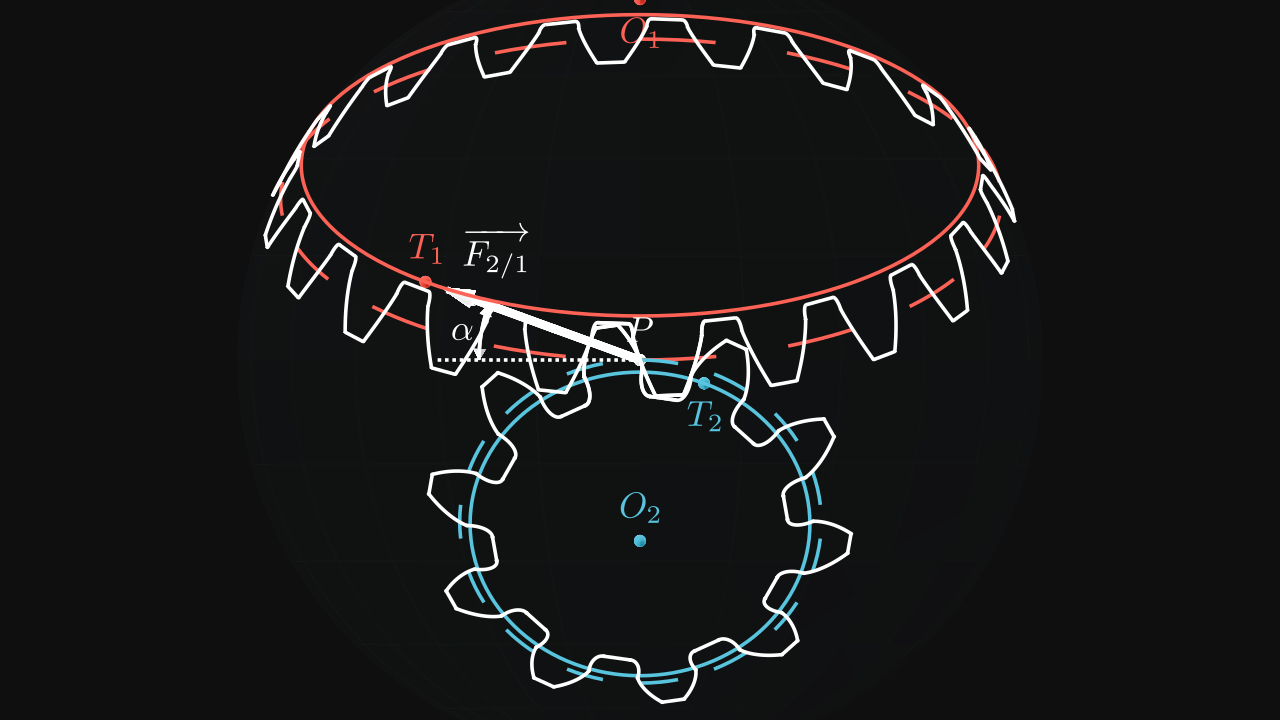
In this part, we are going to code a complete bevel gear profile in Python.
Libraries requires are PyGLM and manim
Spherical involute function
The following code is the translation of the relation:
\[ \overrightarrow{\theta(t, t_0, \gamma)} = \begin{pmatrix} \sin(\gamma) \cos(\sin(\gamma) \cdot t) \cos(t + t_0) + \sin(\sin(\gamma) \cdot t) \sin(t + t_0) \\ \sin(\gamma) \cos(\sin(\gamma) \cdot t) \sin(t + t_0) - \sin(\sin(\gamma) \cdot t) \cos(t + t_0) \\ \cos(\gamma) \cos(\sin(\gamma) \cdot t) \end{pmatrix} \]
from glm import *
from math import *
def spherical_involute(cone_angle:float, t0:float, t:float) -> vec3:
"""
Return spherical involute function
Parameters
----------
t : float
The angular position
t0 : float
The difference phase
cone_angle : float
The cone angle
Returns
-------
vec3
A point on the spherical involute
"""
cos_g, sin_g = cos(cone_angle), sin(cone_angle)
return vec3(
sin_g * cos(t * sin_g) * cos(t + t0) + sin(t * sin_g) * sin(t + t0),
sin_g * cos(t * sin_g) * sin(t + t0) - sin(t * sin_g) * cos(t + t0),
cos_g * cos(t * sin_g),
)Interference function
The following code is the translation of the relation:
\[ \overrightarrow{\theta_{int}(t, t_0, \alpha)} = \cos(\alpha) \cdot \overrightarrow{\theta(t, t_0, \gamma_p)} + \sin(\alpha) \cdot \overrightarrow{\gamma_{int}(t + t_0)} \]
where
\[ \overrightarrow{\gamma_{int}(t)} = \begin{pmatrix} -\cos(\gamma_p) \cos(t) \\ -\cos(\gamma_p) \sin(t) \\ \sin(\gamma_p) \end{pmatrix} \]
from glm import *
from math import *
def spherical_involuteof(
pitch_cone_angle:float, t0:float, alpha:float, t:float
) -> vec3:
"""
Return the spherical interference function
Parameters
----------
t : float
The angular position
t0 : float
The difference phase
pitch_cone_angle : float
The pitch cone angle
alpha : float
The height angle offset of the rack
Returns
-------
vec3
A point on the spherical interference function
"""
cos_p, sin_p = cos(pitch_cone_angle), sin(pitch_cone_angle)
return (
cos(alpha) * spherical_involute(pitch_cone_angle, t0, t)
+ sin(alpha) * vec3(-cos_p * cos(t + t0), -cos_p * sin(t + t0), sin_p)
)The angle \(\beta\) is included in the difference phase \(t_0\).
Intersection between the spherical interference function and the spherical involute function
To get the intersection between both functions, we are going to use the Newton’s Method to solve this problem.
The function that we want to minimize is defined as:
\[ f(t_1, t_2, t_{01}, t_{02}) = \overrightarrow{\theta(t_1, t_{01}, \gamma)} - \overrightarrow{\theta_{int}(t_2, t_{02}, \alpha)} \]
First, we need to differenciate both functions. The derivative of the spherical involute function is:
\[ \overrightarrow{\theta'(t, t_0, \gamma)} = \begin{pmatrix} \cos(\gamma)^2 \sin(\gamma \cdot t) \cos(t + t_0) \\ \cos(\gamma)^2 \sin(\gamma \cdot t) \sin(t + t_0) \\ -\cos(\gamma) \sin(\gamma) \sin(\gamma \cdot t) \end{pmatrix} \]
And the derivative of the spherical interference function is:
\[ \overrightarrow{\theta_{int}'(t, t_0, \alpha)} = \cos(\alpha) \cdot \overrightarrow{\theta'(t, t_0, \gamma_p)} + \sin(\alpha) \begin{pmatrix} \cos(\gamma_p) \sin(t + t_0) \\ -\cos(\gamma_p) \cos(t + t_0) \\ 0 \end{pmatrix} \]
Then we construct the jacobian matrix: \[ J(t_1, t_2, t_{01}, t_{02}) = \begin{pmatrix} \overrightarrow{\theta'(t_1, t_{01}, \gamma)} & -\overrightarrow{\theta_{int}'(t_2, t_{02}, \alpha)} & \vec z \end{pmatrix} \]
The angles \(t_{01}\) and \(t_{02}\) are constants well-known. Only the angles \(t_1\) and \(t_2\) are the variables.
The following code is the translation of these relations:
from glm import *
from math import *
def derived_spherical_involute(cone_angle:float, t0:float) -> callable:
"""
Return the function of the derived spherical involute function.
Parameters
----------
cone_angle : float
The cone angle
t0 : float
The phase difference
Returns
-------
callable
Derived spherical involute function
"""
cos_g, sin_g = cos(cone_angle), sin(cone_angle)
return lambda t: vec3(
cos_g ** 2 * sin(t * sin_g) * cos(t + t0),
cos_g ** 2 * sin(t * sin_g) * sin(t + t0),
-cos_g * sin_g * sin(t * sin_g),
)
def jacobian_spherical_involute(
base_cona_angle:float, pitch_cone_angle:float, t01:float, t02:float, alpha:float
) -> callable:
"""
Return the function of the jacobian used for the newton method in
`spherical_gearprofile`
Parameters
----------
base_cona_angle : float
The base cone angle
pitch_cone_angle : float
The pitch cone angle
t01 : float
The phase of the spherical involute function
t02 : float
The phase of the spherical interference function
alpha : float
The height angle offset of the rack
Returns
-------
callable
Jacobian to get the intersection between the spherical involute
function the spherical interference function
"""
dsi = derived_spherical_involute # for convenience
derived_involute = dsi(base_cona_angle, t01)
cos_p = cos(pitch_cone_angle)
vec = lambda t: vec3(cos_p * sin(t), -cos_p * cos(t), 0)
derived_interference = lambda t: (
dsi(pitch_cone_angle, t02)(t) * cos(alpha) + sin(alpha) * vec(t + t02)
)
return lambda t1, t2: mat3(
derived_involute(t1),
-derived_interference(t2),
vec3(0, 0, 1),
)Rack parameters
Rack parameters are useful better placements or to get dimensions:
from glm import *
from math import *
def spherical_rack_tools(
z:float, pressure_angle:float = pi / 9, ka:float = 1, kd:float = 1.25
):
"""
Return a list of all information useful to generate a spherical rack.
Parameters
----------
z : float
Number of tooth of the rack equal to `z_pinion / sin(pitch_cone_angle)`
or `z_wheel / sin(shaft_angle - pitch_cone_angle)`
pressure_angle : float
The pressure angle of the gear
ka : float
The addendum coefficient
kd : float
The dedendum coefficient
Returns
-------
tuple
* the minimum abscissa for the function (fifth element)
* the maximum abscissa for the function (fifth element)
* the phase of a tooth
* the phase of space
* the function to generate a tooth
"""
k = 1 / z
gamma_p = 0.5 * pi
gamma_b = asin(cos(pressure_angle))
cos_b, sin_b = cos(gamma_b), sin(gamma_b)
gamma_f = gamma_p + atan2(2 * ka * k, 1)
gamma_r = gamma_p - atan2(2 * kd * k, 1)
phi_p = acos(tan(gamma_b) / tan(gamma_p))
theta_p = atan2(sin_b * tan(phi_p), 1) / sin_b - phi_p
phase_diff = k * pi + 2 * theta_p
t_min = acos(cos(gamma_r) / cos_b) / sin_b
t_max = acos(cos(gamma_f) / cos_b) / sin_b
involute = lambda t, t0: spherical_involute(gamma_b, t0, t)
v = vec3(1, 1, 0)
phase_empty = 2 * pi * k - anglebt(
involute(t_min, 0) * v, involute(-t_min, phase_diff) * v
)
return [t_min, t_max, phase_diff, phase_empty, involute]Spherical gear profile
Now we have all of these functions, we can make a spherical gear profile:
from gml import *
from manim import *
from math import *
def spherical_gearprofile(
z:int,
step: float,
pitch_cone_angle:float,
pressure_angle:float = pi / 9,
ka:float = 1,
kd:float = 1.25,
):
"""
Generate 1-period tooth spherical profile for a bevel gear
Parameters
----------
z : int
Number of tooth on the gear this profile is meant for
step : float
Step of a tooth
pitch_cone_angle : float
The pitch cone angle
pressure_angle : float
Pressure angle of the tooth
ka : float
Addendum coefficient
kd : float
Dedendum coefficient
"""
# Initialization of parameters
gamma_p = pitch_cone_angle # for convenience
rp = z * step / (2 * pi)
rho1 = rp / sin(gamma_p)
gamma_b = asin(cos(pressure_angle) * sin(gamma_p))
cos_b, sin_b = cos(gamma_b), sin(gamma_b)
tooth_size = pi / z
involute = lambda t, t0 : spherical_involute(gamma_b, t0, t)
epsilon_p = acos(cos(gamma_p) / cos_b) / sin_b
theta_p = anglebt(
involute(0, 0) * vec3(1, 1, 0), involute(epsilon_p, 0) * vec3(1, 1, 0)
)
phase_diff = tooth_size + 2 * theta_p
phase_empty = phase_interference = 2 * pi / z - phase_diff
# The following number `k` is useful to simplify some calculations
# It's broadly speaking `1/z_rack` and `z_rack` is not an integer !
k = sin(gamma_p) / z
# Spherical involute part
gamma_f = gamma_p + atan2(2 * ka * k, 1) # addendum cone angle
gamma_r = gamma_p - atan2(2 * kd * k, 1) # dedendum cone angle
t_min = 0
t_max = acos(cos(gamma_f) / cos_b) / sin_b
if gamma_r > gamma_b:
v = vec3(1, 1, 0)
t_min = acos(cos(gamma_r) / cos_b) / sin_b
phase_empty = 2 * pi / z - anglebt(
involute(t_min, 0) * v, involute(-t_min, phase_diff) * v
)
# Calculation of offsets due to geometry of spherical rack
_, t_rack_max, phase1, _, rinvolute = spherical_rack_tools(
1 / k, pressure_angle, ka, kd
)
interference = lambda t, t0 : spherical_involuteof(gamma_p, t0, alpha, t)
alpha = atan2(2 * ka * k, 1)
n1 = rinvolute(t_rack_max, 0) * vec3(1, 1, 0)
n2 = rinvolute(-t_rack_max, phase1) * vec3(1, 1, 0)
beta = 0.5 * anglebt(n1, n2) * length(n1) / sin_b
# Newton method to calculate the intersection between
# the spherical involute and the spherical interference.
# Objective function
involuteat = lambda t2, t0 : spherical_involuteof(gamma_p, t0, alpha, t2)
f = lambda t1, t2: (
involute(t1, 0) - involuteat(t2, -0.5 * phase_interference + beta)
)
# Jacobian matrix
J = jacobian_spherical_involute(
gamma_b, gamma_p, 0, -0.5 * phase_interference + beta, alpha
)
# Compute the intersection values
t1, t2, t3 = 0.5 * t_max, -0.5 * t_max, 0
for i in range(8):
t1, t2, t3 = vec3(t1, t2, t3) - inverse(J(t1, t2)) * f(t1, t2)
# Build sides of a tooth
interference1 = ParametricFunction(
lambda t: rho1 * interference(t, -0.5 * phase_interference + beta),
t_range=[t2, 0],
)
interference2 = ParametricFunction(
lambda t: rho1 * interference(
-t, phase_diff + 0.5 * phase_interference - beta
),
t_range=[t2, 0],
)
side1 = ParametricFunction(
lambda t: rho1 * involute(t, 0), t_range=[t1, t_max]
)
side2 = ParametricFunction(
lambda t: rho1 * involute(-t, phase_diff), t_range=[t1, t_max]
)
# Extreme points of sides to compute angle between them
a = rho1 * interference(0, -0.5 * phase_interference + beta)
b = rho1 * interference(0, phase_diff + 0.5 * phase_interference - beta)
final_phase_empty = 2 * pi / z - anglebt(a * vec3(1, 1, 0), b * vec3(1, 1, 0))
top = Line(rho1 * involute(t_max, 0), rho1 * involute(-t_max, phase_diff))
bottom = Line(rotate(-final_phase_empty, vec3(0, 0, 1)) * a, a)
aligned_phase = anglebt(
(
rho1 * involute(t_max, 0) + rho1 * involute(-t_max, phase_diff)
) * 0.5 * vec3(1, 1, 0),
X,
)
return VGroup(
interference1,
interference2,
side1,
side2,
top,
bottom,
Dot(a, radius=0.03),
Dot(b, radius=0.03),
Dot(rho1 * involute(t1, 0), radius=0.03),
Dot(rho1 * involute(t_max, 0), radius=0.03),
Dot(rho1 * involute(-t1, phase_diff), radius=0.03),
Dot(rho1 * involute(-t_max, phase_diff), radius=0.03),
).rotate_about_origin(-aligned_phase, Z)One last function
The last function is get_pitch_cone_angle to determine the pitch cone angle given the number of teeth of the wheel and those of the pinion:
from math import *
def get_pitch_cone_angle(
z_pinion: int, z_wheel: int, shaft_angle: float = 0.5 * pi
) -> float:
"""
Return the pitch cone angle of the pinion called `gamma_p`.
The pitch cone angle of the wheel is equal to `shaft_angle - gamma_p`.
Parameters
----------
z_pinion : int
The number of teeth on the bevel pinion
z_wheel : int
The number of teeth on the bevel wheel
shaft_angle : float
The shaft angle
Returns
-------
float
The pitch cone angle
"""
return atan2(sin(shaft_angle), ((z_wheel / z_pinion) + cos(shaft_angle)))Example to make a spherical gear profile
z_pinion = 10
z_wheel = 20
m = 0.5
step = pi * m
pressure_angle = pi / 9
pitch_cone_angle = get_pitch_cone_angle(z_pinion, z_wheel)
gamma_p = pitch_cone_angle # for convenience
rp = z_pinion * step / (2 * pi)
rho1 = rp / sin(gamma_p)
angle1tooth_pinion = 2 * pi / z_pinion
def revolution(vgroup, angle, times):
final_vgroup = vgroup.copy()
for i in range(times):
rotated_vgroup = vgroup.copy().rotate_about_origin(angle * i)
for line in rotated_vgroup:
final_vgroup += line
return final_vgroup
pinion_profile = revolution(
spherical_gearprofile(z_pinion, step, pitch_cone_angle),
angle1tooth_pinion,
z_pinion,
)
angle1tooth_wheel = 2 * pi / z_wheel
wheel_profile = revolution(
spherical_gearprofile(z_wheel, step, pi / 2 - pitch_cone_angle),
angle1tooth_wheel,
z_wheel,
)Bonus : spherical rack profile
Remember that the spherical rack does not have an integer number of teeth. The number of teeth of the rack is:
\[ z_{\text{rack}} = \frac{z_{\text{pinion}}}{\sin([\text{pitch cone angle}]_{\text{pinion}})} \]
Here is the code to make a spherical rack profile:
z = z_pinion = 10
z_wheel = 20
m = 0.5
step = pi * m
pressure_angle = pi / 9
ka = 1
kd = 1.25
pitch_cone_angle = get_pitch_cone_angle(z_pinion, z_wheel)
gamma_p = pitch_cone_angle # for convenience
gamma_b = asin(cos(pressure_angle) * sin(gamma_p))
rp = z_pinion * step / (2 * pi)
rho1 = rp / sin(gamma_p)
t_min, t_max, phase1, phase2, involute = spherical_rack_tools(z, pressure_angle, ka, kd)
def revolution(vgroup, angle, times):
final_vgroup = vgroup.copy()
for i in range(times):
rotated_vgroup = vgroup.copy().rotate_about_origin(angle * i)
for line in rotated_vgroup:
final_vgroup += line
return final_vgroup
side1 = ParametricFunction(
lambda t: rho1 * involute(t, 0), t_range=[t_min, t_max]
)
side2 = ParametricFunction(
lambda t: rho1 * involute(-t, phase1), t_range=[t_min, t_max]
)
rack = VGroup(
side1,
side2,
Line(rho1 * involute(t_min, -phase2), rho1 * involute(t_min, 0)),
Line(rho1 * involute(t_max, 0), rho1 * involute(-t_max, phase1)),
) # one tooth
# The rack is upside down
# You can add .rotate(pi, X, about_point=O) to `rack` if you want to rotate it
# properly
rack = revolution(
rack,
anglebt(
involute(t_min, -phase2) * (X + Y),
involute(-t_min, phase1) * (X + Y),
),
5 # arbitrary number of teeth
)